Sphere on a freely spinning turntable

Steve Mould somewhat recently published a video of a sphere rolling on a turntable rotating at constant rate and demonstrated that the path of the ball is, quite surprisingly, a circle. This demonstration was based on a 1978 paper titled Stable circular orbits of freely moving balls on rotating discs, Klaus Weltner. The same problem was also solved in Harvard Physics forum as Ball on turntable.

Its even more amazing that the path of a spherical ball rolling on a freely spinning turntable is a conic section as shown in A ball on a freely spinning turntable, Warren Weckesser [1]. Weckesser's request for a geometric derivation was answered about 20 years later in Comment on "A ball on a freely spinning turntable", Luis Rodriguez. A 2011 paper by Hector Munera titled A ball rolling on a freely spinning turntable: Insights from a solution in polar coordinates [2] further discusses some aspects that were not covered previously.

In this post, we aim to show 'the cone and the plane' of the conic section which has not been noted in any of the quoted papers. The key equations we need are (11) and (5) of [2] which we note here for ease.

$\displaystyle\Omega^2=\frac{\delta+\alpha r_0^2}{\delta+\alpha r^2}$ and $\mathbf{r}'=\alpha\Omega\mathbf{k}\times\mathbf{r}+\mathbf{c}$

For our purposes, we slightly alter these expression by differentiating the second and using some algebraic manipulations in the first.

$\displaystyle\Omega^2\left(\frac{\delta}{\alpha}+r^2\right)=\Omega_0^2\left(\frac{\delta}{\alpha}+r_0^2\right)$ and $\mathbf{r}''=\alpha\mathbf{k}\times(\Omega\mathbf{r})'$

Note that $\Omega_0=1$ by definition and therefore will be ignored at will from now on in this post.

To bring the cone out from hiding, we take the problem to the third dimension. To this end, we define

$\mathbf{p}=\mathbf{r}+\sqrt{\delta/\alpha} \text{ } \mathbf{k}$

Then, our two equations become

$\Omega p=\Omega_0p_0$  and $\mathbf{p}''=\alpha p_0 \mathbf{k}\times\widehat{\mathbf{p}}'$

where $p=|\mathbf{p}|$.

Because $\mathbf{p}$ and $\mathbf{r}$ are just a translation away, they have the same shape. Also, because of our definition of $\mathbf{p}$, we know that the curve defined by $\mathbf{p}$ lies on a plane perpendicular to the z-axis.

We also like to highlight that because of the definition of $\mathbf{p}$, the derivatives of $\mathbf{p}$ and $\mathbf{r}$ coincide and because $\mathbf{r} \cdot \mathbf{k}=0$, the derivatives of $\mathbf{p}$ are also perpendicular to $\mathbf{k}$.

Now we define a new vector $\mathbf{m}$ such that

$\mathbf{m}=\mathbf{p}\times\mathbf{p}'+\sqrt{\delta\alpha}p_0\text{ }\widehat{\mathbf{p}}$

Surprisingly, $\mathbf{m}$ is a constant of motion. This can be proved in multiple ways of which we show one here.

$\begin{align}(\mathbf{p}\times\mathbf{p}')' &= \mathbf{p}\times\mathbf{p}'' \\ &= \mathbf{p}\times (\alpha p_0 \mathbf{k} \times \widehat{\mathbf{p}}') \\ &= \alpha p_0 \bigl[ (\mathbf{p}\cdot\widehat{\mathbf{p}}')\mathbf{k}-(\mathbf{p}\cdot\mathbf{k})\widehat{\mathbf{p}}'\bigr] \\ &= -\sqrt{\delta\alpha} p_0\text{ }\widehat{\mathbf{p}}' \end{align}$

and therefore $\mathbf{m}'=(\mathbf{p}\times\mathbf{p}'+\sqrt{\delta\alpha} p_0\text{ }\widehat{\mathbf{p}})'=\mathbf{0}$.

We have used the fact that $\mathbf{q}\cdot\widehat{\mathbf{q}}'=0$ for any vector $\mathbf{q}$ because

$\displaystyle \widehat{\mathbf{q}}'=\frac{(\mathbf{q}\times\mathbf{q}')\times \mathbf{q}}{|\mathbf{q}|^3}$

Now that we know $\mathbf{m}$ is a constant vector, we can also easily see that $\widehat{\mathbf{p}}\cdot \mathbf{m}=\sqrt{\delta\alpha}p_0$, a constant which shows that the unit vectors of $\mathbf{p}$ have the same angle with $\mathbf{m}$ at all times.

Using these facts, we can finally see that the conic section that results from the path of the ball is the intersection of the $z=\sqrt{\delta/\alpha}$ plane and the cone whose vertex is the origin, $\mathbf{m}$ as its axis and $\mathbf{p} _0$ at its generator.

While the constancy of $\mathbf{m}$ could've been derived directly from (1), (4) and (5) of [2], taking the problem to the third dimension brings out the cone in the conic just beautifully.

Update (28-Mar-25)

The expression for $\mathbf{m}$ can rewritten as

$\mathbf{p}\times\mathbf{p}'=\mathbf{m}-\sqrt{\delta\alpha}p_0\text{ }\widehat{\mathbf{p}}$

As $\mathbf{m}$ is constant and $\widehat{\mathbf{p}}$ traces a circle with its axis along  $\mathbf{m}$, we note that the magnitude of the RHS of the above expression is a constant.

Therefore,

$|\mathbf{p}\times\mathbf{p}'|=|\mathbf{p}_0\times\mathbf{p}'_0|$

Since the cross product of two vectors gives the area of the parallelogram with the two vectors as its side, the curved surface of the cone $dA$ swept in time $dt$ is given by,

$\displaystyle \frac{dA}{dt}=\frac{1}{2}|\mathbf{p}\times\mathbf{p}'|=\frac{1}{2}|\mathbf{p}_0\times\mathbf{p}'_0|$

This shows the 'areal velocity' of $p$ is constant, much like that of the Kepler's laws of planetory motion. In particular, the orbital period $T$ of the sphere rolling on a freely spinning turntable is given by,

$\displaystyle T=\frac{A}{\frac{1}{2}|\mathbf{p}_0\times\mathbf{p}'_0|}$

The curved surface $A$ of the cone can be calculated using the formula given in Finkel's Solution Book as referenced in Problem 336, Mar 1914, American Mathematical Monthly.

To the best of my knowledge, this seems to be first time that an explicit expression for the time period of a sphere rolling on a freely spinning turntable!

Hope you enjoyed the discussion. See ya later.

Until then

Yours Aye

Me

An interesting Probability problem

I recently came across an interesting problem concerning the probability of a random sphere lying inside an unit ball in stackexchange.

The solution methodology was so fascinating that inspired me to come up with the following, almost similar, problem: Given a triangle and three points selected uniformly randomly from the triangle, what is the probability that the circle passing through those points lie completely inside the triangle?

We can characterise the three points the same way as in the SE post. Then,

$\displaystyle\mathbb{P}(\text{circle inside triangle})=\frac{1}{A^3}\iiint\limits_{\sqrt{x^2+y^2}+r \in \triangle}\,dx\,dy\,dr\int\limits_0^{2\pi}\int\limits_0^{2\pi}\int\limits_0^{2\pi}\frac{\partial (x_1,y_1,x_2,y_2,x_3,y_3)}{\partial (x,y,r,\phi_1,\phi_2,\phi_3)}\,d\phi_1\,d\phi_2\,d\phi_3$

where $A$ is the area of the given triangle $\triangle$ and the coordinates $(x,y)$ are w.r.t some arbitrary origin.

The integral involving $\phi$'s can be handled the same way as shown in the SE post which reduces the above expression to,

$\begin{align}\displaystyle\mathbb{P}(\text{circle inside triangle}) &= \frac{1}{A^3}\cdot (2\pi)^3\cdot 2 \cdot \frac{3}{2\pi}\iiint\limits_{\sqrt{x^2+y^2}+r \in \triangle}r^3 \,dx\,dy\,dr \\ &= \frac{24\pi^2}{A^3}\iiint\limits_{\sqrt{x^2+y^2}+r \in \triangle}r^3 \,dx\,dy\,dr \\ \end{align}$

If we now choose the incenter of the triangle to be the origin and $R$ to be inradius of the triangle, then the integral above w.r.t $\,dx\,dy$ is just the area of the set of points that are at the distance of $r$ inward from the triangle. But that is just the same triangle scaled such that its inradius is $R-r$. That is,

$\displaystyle \iint\limits_{\sqrt{x^2+y^2}+r \in \triangle}\,dx\,dy=\left(1-\frac{r}{R}\right)^2\cdot A$

Therefore,

$\begin{align}\displaystyle\mathbb{P}(\text{circle inside triangle}) &= \frac{24\pi^2}{A^3}\int\limits_0^R \left(1-\frac{r}{R}\right)^2\cdot A\,dr \\ \end{align}$

Evaluating this simple integral, we finally get,

$\displaystyle \mathbb{P}(\text{circle inside triangle}) = \frac{2}{5}\left(\frac{\pi R^2}{A}\right)^2$

A similar approach can be used to find the probability that a circle formed by choosing two points uniformly randomly inside a triangle completely lies within the triangle. In this case,

$\displaystyle \mathbb{P}(\text{circle inside triangle}) = \frac{2}{3}\frac{\pi R^2}{A}$

It should be easy to see from here that the above formulas, in fact, works for any tangential polygon. If we take it a step further, the same approach can be made to work for any closed convex curve. The only tricky part is the integral w.r.t '$\,dx\,dy$' which would now be the area enclosed by the 'inward' parallel curve of the given curve, which is not terribly difficult but isn't straightforward either.

An equally interesting but a tad more challenging problem is the following: Choose two points uniformly randomly inside a given triangle. If we now construct the square with the line joining the chosen points as the diagonal, what is the probability that the square lies within the triangle?

We'll see this problem in a separate post. If you figure out the answer, please share it with us in the comments section below.

Until then

Yours Aye

Me

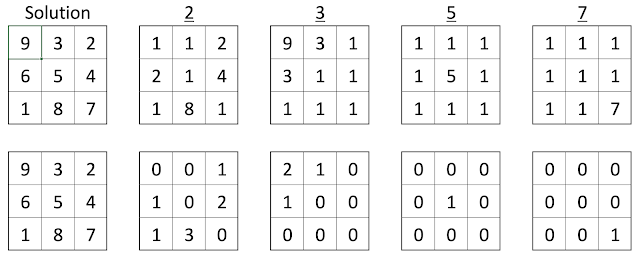
Monkey Dog Problem - Grid Multiplication

The following problems was recently posted in the IIM-Cal puzzle group (and eventually in my puzzle group as well): Can we fill an $n \times n$ grid with the first $n^2$ integers such that the product of the numbers in the $k$th row equals that of the $k$th column for $1 \leq k \leq n$?

The fact that this is impossible for $n=2$ is easy to show by inspection. Vamshi Jandhyala in our group posted grids with the required property for $3 \times 3$ and $4 \times 4$ (and eventually for $10 \times 10$) using a Python non-linear solver. However, this approach ended up time-expensive for larger grids.

He also showed such grids are impossible whenever $n=9$ or $n>10$ using a nice argument involving the number of primes between $n^2/2$ and $n^2$.

Not wanting to get into the realm of non-linearity, I log'ed the entire grid so that multiplication becomes addition and the problem becomes linear. Note that this made an Integer Non-Linear problem to a Non-Integer Linear problem. Despite precision errors, this approach worked for $n=3,4$ but proved elusive for larger $n$.

Running out of options, I eventually realised that each grid that satisfies the required property can be seen only for a particular prime (their exponents in all the $n^2$ numbers to be specific) while ignoring others.

The top half of the above snapshot shows a solution to a $3 \times 3$ grid for a particular prime. The bottom half shows the same but in terms of the exponents of the prime.

The prime exponents form makes it clear that the problem can indeed be modelled as an Integer Linear Problem which can be solved extremely efficiently using free solvers in Python. In fact, doing so enables us to solve the problem for all the cases in a matter of seconds.

A Solution for $5 \times 5$ grid

A Solution for $6 \times 6$ grid

A Solution for $7 \times 7$ grid

A Solution for $8 \times 8$ grid

Python code used for solving this problem.

from ortools.linear_solver import pywraplp
import numpy as np


def main():
    # Data
    n = 3
    vals = []
    # primes = [2, 3, 5, 7, 11, 13, 17, 19, 23]
    # primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]
    # primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61]
    primes = [2, 3, 5, 7]
    primepi = len(primes)
    
    def vals(i0, k):
        i, cnt, p = i0, 0, primes[k]
        while i % p == 0:
            i //= p
            cnt += 1
        return cnt

    # Solver
    # Create the mip solver with the SCIP backend.
    solver = pywraplp.Solver.CreateSolver("SCIP")

    x = {}
    for i in range(n * n):
        for j in range(n * n):
            x[i, j] = solver.IntVar(0, 1, "")
    
    for i in range(n * n):
        solver.Add(solver.Sum([x[i, j] for j in range(n * n)]) == 1)
    
    for j in range(n * n):
        solver.Add(solver.Sum([x[i, j] for i in range(n * n)]) == 1)
    
    y = {}
    for i in range(n * n):
        for k in range(primepi):
            y[i, k] = solver.Sum([x[i, j] * vals(j + 1, k) for j in range(n * n)])

    
    rowsum = {}
    for i in range(n):
        for k in range(primepi):
            rowsum[i, k] = solver.Sum([y[j, k] for j in range(n * i, n * i + n)])
    
    colsum = {}
    for i in range(n):
        for k in range(primepi):
            colsum[i, k] = solver.Sum([y[j, k] for j in range(i, n * n, n)])
    
    for i in range(n):
        for k in range(primepi):
            solver.Add(rowsum[i, k] == colsum[i, k])
    
    solver.Minimize(1)
    status = solver.Solve()

    # Print solution.
    if status == pywraplp.Solver.OPTIMAL or status == pywraplp.Solver.FEASIBLE:
        res = []
        for i in range(n * n):
            for j in range(n * n):
                if x[i, j].solution_value() > 0:
                    res += [j + 1]
        print(res)
    else:
        print("No solution found.")


if __name__ == "__main__":
    main()

That eventually settles the Monkey Dog Problem of Grid multiplication. There is also an interesting question of finding $n$ which has the lowest number of solutions if rotations and reflections are identified. That could be left as an exercise to the reader.

Hope you enjoyed this. See ya later.

Until then

Yours Aye

Me

Five ways of solving an Expected Value problem

 Let's say an Independent Aurelian is investigating butterflies on two types of traits, A and B. It is known that the probability of a butterfly exhibiting trait A is $p$ and that of trait B is $q$ (independent of each other). Note that this means the probability of a butterfly exhibiting both these traits is $pq$.

If she wants to study both these traits, how many butterflies, on average, would she need to catch? She can do this either by catching two butterflies each with exactly on of these traits or by catching a butterfly with both these traits.

The problem is simple and that subject of this post is look at five different methods of this problem. A key fact that will be of great use in all these methods is that for an event with success probability $r$, we would need, on average, $1/r$ trials to get the first success.

Simple equation

Let $N$ be the expected value we are looking for. We can condition this based on the nature of the first butterfly that is caught.

$\displaystyle N=(1-p)(1-q)\cdot(1+N)+(1-p)q\cdot \left(1+\frac{1}{p}\right)+p(1-q)\cdot\left(1+\frac{1}{q}\right)+pq\cdot 1$

Transfer Matrix

It is easy to setup the transfer matrix for this problem with the states being $\{\text{None, Only trait }A\text{, Only trait }B\text{, Both}\}$. Then the transfer matrix $\mathbf{T}$ is,

$\displaystyle \mathbf{T}=\begin{pmatrix}1-(1-p)(1-q)&p(1-q)&(1-p)q&pq \\ 0&1-q&0&q \\ 0&0&1-p&p \\ 0&0&0&1\end{pmatrix}$

It is then well known that the expected value is given by $\mathbf{1}(\mathbf{I}-\mathbf{T})^{-1}$ where $\mathbf{I}$ is the identity matrix and $\mathbf{1}$ is a row matrix of 1's.

Infinite Series

Let's say we've caught $n$ butterflies. The probability that none of them have trait A is $(1-p)^n$ which means that atleast one of them have trait A is $1-(1-p)^n$ and the same applies for trait B as well (with $p$ replaced with $q$).

$\mathbb{P}(\text{atleast of one each of both traits in }n\text{ trials})=(1-(1-p)^n)(1-(1-q)^n)$

With this, we see that $\mathbb{P}(N>n)=1-(1-(1-p)^n)(1-(1-q)^n)$

Then, $\displaystyle \mathbb{E}(N)=\sum_{n=0}^\infty \mathbb{P}(N>n)=\sum_{n=0}^\infty \Bigl (1-(1-(1-p)^n)(1-(1-q)^n) \Bigl )$

Story proof

We can answer this more directly. The expected number of butterflies needed can be broken into parts. First, expected number to get atleast one of the traits and second, the remaining value.

The probability of a butterfly exhibiting one of the traits is $1-(1-p)(1-q)=p(1-q)+(1-p)q+pq$. Therefore, we would need $1/(1-(1-p)(1-q))$ trials to get atleast of the traits. Now,

$\displaystyle \mathbb{P}(\text{Only trait A}|\text{atleast one of the traits})=\frac{p(1-q)}{p(1-q)+(1-p)q+pq}=\frac{p(1-q)}{1-(1-p)(1-q)}$

After having got trait A, we would be looking for trait B which we would get, on average, in $1/q$ trails. This approach applies for the other two cases as well. Therefore,

$\displaystyle\mathbb{E}(N)=\frac{1}{1-(1-p)(1-q)}+\frac{p(1-q)}{1-(1-p)(1-q)}\cdot\frac{1}{q}+\frac{(1-p)q}{1-(1-p)(1-q)}\cdot\frac{1}{p}+\frac{pq}{1-(1-p)(1-q)}\cdot 0$

(Shorter story proof using) Min-Max identity

It is easy to see that $x_1+x_2=\max (x_1,x_2)+\min (x_1,x_2)$ for any two real $x_1,x_2$.

Using this and the linearity of expectations, we have,

$\mathbb{E}(N)=\mathbb{E}(\text{trials to get trait A})+\mathbb{E}(\text{trials to get trait B})-\mathbb{E}(\text{trials to get atleast one of the traits})$

All of these are Geometric random variables with probabilities $p$, $q$ and $p+q-pq$. Therefore,

$\displaystyle \mathbb{E}(N)=\frac{1}{p}+\frac{1}{q}-\frac{1}{p+q-pq}$

Where's the fun in solving a problem if getting an answer is the only objective?

Yours Aye

Me

A Geometric Optimisation problem

Consider two circles $A(B)$ and $C(B)$ intersecting at $B$ and $D$, and a line passing through $D$. Let this line intersect the circle $A(B)$ at $F$ and the circle $C(B)$ at $G$.

The question of maximising the arithmetic mean of $DF$ and $DG$ is well known. It is also known that Euclidean construction of the line that maximises the Harmonic mean of $DF$ and $DG$ is impossible. We already saw the construction of the line that maximises the Geometric mean of $DF$ and $DG$ in this blog.

In this post we are interested in constructing the line such that the Quadratic mean of $DF$ and $DG$ is maximised. In fact, we solve a slightly more general problem. For a given $\theta$, we construct the line such that $\sqrt{DF^2+DG^2-2 \cdot DF \cdot DG \cdot \cos \theta}$ is maximised.

We first use some auxiliary points and lines that helps us in the final solution. For a given $\theta$, construct points $D'$ and $D'_1$ such that $\angle DAD'=\angle DCD'_1=\theta$. Construct the circle that passes through $D$, $B$ and $D'_1$.

For any point $E$ on this circle, let the line $ED'$ intersect circle $A(B)$ at $F$. Let $G$ be likewise on circle $C(B)$. Construct line $FG$. We first show that the line $FG$ passes through $D$.

We know that $\angle FD'B+\angle FDB=\pi$ because they are opposite angles in a cyclic quadrilateral. But $\angle FD'B=\angle ED'B=\pi-\angle ED'_1B$ because $\angle ED'B$ and $\angle ED'_1B$ are opposite angles of a cyclic quadrilateral. Now, $\angle FD'B=\angle BD'_1G=\angle BDG$.

Therefore, $\angle BDG + \angle FDB=\pi$ which shows that $F$, $D$ and $G$ are collinear.

Now, by construction, $\theta / 2=\angle D'BD=\angle D'_1BD$ and therefore, $\angle D'BD'_1=\theta$. This shows that $\angle D'ED'_1=\pi-\theta$.

We know that $\angle DGD'_1=\angle DBD'_1=\theta/2$ because they are angles in a same segment of a circle. Because $\angle DAD'=\theta$, we can see that $\angle DFD'=\pi-\theta/2$, and therefore $\angle DFE=\theta/2$.

Thus we have shown that $\triangle FEG$ is isosceles with $FE=EG$. Therefore, we can quickly see that $FG=2EF\cos(\theta/2)$.

Using Stewart's theorem on this triangle for the cevian DE, we have,

$EF^2=DE^2+DF\cdot DG$

Multiplying by $(2\cos(\theta/2))^2$ on both sides and simplifying, we get

$(2\cos(\theta/2))^2DE^2=FG^2-2DF\cdot DG \cdot 2\cos^2(\theta/2)$

Using the fact that $FG=DF+DG$ and $\cos\theta=2\cos^2(\theta/2)-1$,

$(2\cos(\theta/2))^2DE^2=DF^2+DG^2-2\cdot DF \cdot DG \cdot \cos\theta$

As $\theta$ is given, the above expression shows that maximising the RHS amounts to maximising $DE$. But this can be easily achieved. We just draw the line joining $D$ and center of circle $D'BD'_1$. The point at which this line intersects the circle gives us $E$ from which we can trivially construct the line $FG$ using what we've described before.

Hope you enjoyed this. See ya soon.

Until then, Yours Aye

Me

An Odd Sum

Someone in our puzzle group recently posted a question which asked to evaluate the following sum.

$$\frac{1}{e^{\pi}+1}+\frac{3}{e^{3\pi}+1}+\frac{5}{e^{5\pi}+1}+\cdots$$

My first instinct was to check the sum with Wolfram Alpha which showed me that this sum equals $1/24$. This made me curious.

I recast the sum into the following form.

$$\frac{e^{-\pi}}{1+e^{-\pi}}+\frac{3e^{-3\pi}}{1+e^{-3\pi}}+\frac{5e^{-5\pi}}{1+e^{5\pi}}+\cdots$$

The individual terms reminded me of Lambert series which eventually led me into rabbit hole that is to be the content of this post.

Let's define the following function $f(q)$ such that

$\displaystyle f(q)=\frac{q}{1+q}+\frac{3q^3}{1+q^3}+\frac{5q^5}{1+q^5}+\cdots$

Then,

$\displaystyle -f(-q)=\frac{q}{1-q}+\frac{3q^3}{1-q^3}+\frac{5q^5}{1-q^5}+\cdots$

Expanding using the lambert series for divisor functions, we see

$\displaystyle -f(-q)=\sigma_{\text{odd}}(1)q+\sigma_{\text{odd}}(2)q^2+\sigma_{\text{odd}}(3)q^3+\cdots=\sum_n \sigma_{\text{odd}}(n)q^n$

where $\sigma_{\text{odd}}(n)$ where is sum-of-odd-divisors function.

The sum-of-odd-divisors functions is intimately tied to the number of representations of an integer by a sum of four squares (Jacobi four square theorem) and by sum of four triangular numbers (Legendre). See Analogues on two classical theorems on representations of a number and The Parents of Jacobi’s Four Squares Theorem Are Unique, for example.

Therefore,

$\begin{align} \displaystyle -f(-q) &= \sum_n \sigma_{\text{odd}}(n)q^n \\ &=\frac{1}{24} \left[8\sum_{n\text{ odd}}\sigma_{\text{odd}}(n)q^n + 24\sum_{n\text{ even}}\sigma_{\text{odd}}(n)q^n + 16\sum_{n\text{ odd}}\sigma_{\text{odd}}(n)q^n \right] \\ &= \frac{1}{24}\left(\sum_n r_4(n)q^n+\sum_n t_4(n) q^n \right) \\ &= \frac{\vartheta_2(q)^4+\vartheta_3(q)^4-1}{24}\end{align}$

where $r_4(n)$ (and $t_4(n)$) is the sum-of-four-squares (and sum-of-four-triangulars) function, and $\vartheta_3(q)$ (and $\vartheta_2(q)$) is the third (and second) Jacobi elliptic function.

It is well known that

$\displaystyle \vartheta_3(q)=\sum_{n=-\infty}^\infty q^{n^2}=\phi(q^2)\prod_{n \text{ odd}}(1+q^n)^2$ and 

$\displaystyle \vartheta_2(q)=\sum_{n=-\infty}^\infty q^{(n+1/2)^2}=2\phi(q^2)q^{1/4}\prod_{n \text{ even}}(1+q^n)^2$

where $\displaystyle\phi(q)=\prod_{n}(1-q^n)$ is the Euler function.

Note that

$\displaystyle \prod_{n\text{ odd}}(1-q^n)=\frac{\phi(q)}{\phi(q^2)}$ and $\displaystyle \prod_{n}(1+q^n)=\frac{\phi(q^2)}{\phi(q)}$

Therefore,

$\displaystyle \vartheta_3(-q)=\phi(q^2)\frac{\phi(q)}{\phi(q^2)}\frac{\phi(q)}{\phi(q^2)}$ and $\displaystyle \vartheta_2(-q)=2\phi(q^2)(-q)^{1/4}\frac{\phi(q^4)}{\phi(q^2)}\frac{\phi(q^4)}{\phi(q^2)}$

Now,

$\displaystyle\sqrt\frac{\vartheta_2(-q)}{\vartheta_3(-q)}=\sqrt{2}(-q)^{1/8}\frac{\phi(q^4)}{\phi(q)}$

Putting $q=e^{-\pi}$ in the above expression, we have

$\displaystyle\sqrt\frac{\vartheta_2(-e^{-\pi})}{\vartheta_3(-e^{-\pi})}=\sqrt{2}(-1)^{1/8}e^{-\pi/8}\frac{\phi(e^{-4\pi})}{\phi(e^{-\pi})}$

Using the special values of the Euler function, we see that $\displaystyle \phi(e^{-4\pi})=\frac{e^{\pi/8}}{\sqrt{2}}\phi(e^{-\pi})$

Then,

$\displaystyle\sqrt\frac{\vartheta_2(-e^{-\pi})}{\vartheta_3(-e^{-\pi})}=(-1)^{1/8} \implies \vartheta_2(-e^{-\pi})^4+\vartheta_3(-e^{-\pi})^4=0$

Returning to our expression for $f(q)$, we see that $24f(e^{-\pi})=1-\vartheta_2(-e^{-\pi})^4-\vartheta_3(-e^{-\pi})^4=1$

As $f(e^{-\pi})$ is essentially the sum that we started with, we finally see that

$$\displaystyle\frac{1}{e^{\pi}+1}+\frac{3}{e^{3\pi}+1}+\frac{5}{e^{5\pi}+1}+\cdots=\frac{1}{24}$$

Phew!

As an aside, we could probably arrive the result a little quicker by using some results like

$\displaystyle\lambda(-1+i)=\frac{\vartheta_2(e^{(-1+i)\pi})^4}{\vartheta_3(e^{(-1+i)\pi})^4}=\frac{\vartheta_2(-e^{-\pi})^4}{\vartheta_3(-e^{-\pi})^4}=-1$ (or) $G_1=1\text{ and }g_1=2^{-1/8}$

where $\lambda(n)$ is the Modular lambda function and $g\text{ and }G$ are the Ramanujan g- and G- functions. But I didn't want to bring in additional exotic functions into the problem especially when I can't find a source for the above values of these functions.

Hope you enjoyed this. See ya soon.

Until then, Yours Aye

Me

Tautochronous tanks

Toricelli's law states that the velocity of a discharge, say $v$, located at the bottom of a tank filled to a height $h$ is $v=\sqrt{2gh}$.

Assuming the shape of the tank to be a right prism (with its axis along the $y$-axis), we can use the conservation of mass (or volume in this context) to get

$A \,dy=-a \cdot \sqrt{2gy}\,dt$

where $A$ is the cross sectional area of the prism and $a$ is the area of discharge. Note that the negative sign indicates that $y$ (the height of the water column) decreases as time $t$ increases.

Rearranging and integrating, we have

$\displaystyle \int_0^T \,dt=-\frac{A}{a\sqrt{2g}}\int_h^0 \frac{1}{\sqrt{y}}\,dy \implies T=\frac{A}{a}\sqrt{\frac{2h}{g}}$

where $T$ is the total time taken to drain the tank which is proportional to the square root of the height of the liquid column.

But can we design a tank such that the time of discharge is directly proportional to height? If we assume that the shape of the tank is a solid of revolution such that the area of the cross section at $y$ is given by $A(y)$, then by the similar reasoning as above, we have

$\displaystyle T=\frac{1}{a\sqrt{2g}}\int_0^h \frac{A(y)}{\sqrt{y}}\,dy$

Therefore, for $A(y)=\pi x^2 \propto \sqrt{y}$ (or) $x \propto \sqrt[4]{y}$, we get that $T(h)$ is directly proportional to $h$.

This clearly shows that the draining time for a tank formed by the solid of revolution quartic curve $y=x^4$ is directly proportional to height of the liquid column.

This naturally leads to the second question that we want to address in this post. Can we design a tank such that the draining time is independent of the height of the liquid column.

A direct attack (for example, using Abel's solution of the Tautochrone curve) quickly suggests that there is no such curve.

This might seem like a dead end and it sort of is. But, Let's consider an almost similar question: Can we design a tank, initially filled to the brim, such that the time of discharge is independent of the height at which the discharging hole is located?

For ease of what follows, we orient the coordinate system such that gravity points in the positive $y$ direction. Then for a tank whose shape is a solid of revolution, using the conservation of volume, we have,

$\displaystyle A(y)\,dy=a\cdot \sqrt{2g(y_0-y)}\,dt \implies T(y_0)=\frac{1}{a\sqrt{2g}}\int_0^{y_0}\frac{A(y)}{\sqrt{y_0-y}}\,dy$

where $y_0$ is the height at which the discharge is located.

Now, if we use Abel's idea, we can see that

$\displaystyle A(y)=T_0\frac{a\sqrt{2g}}{\pi}\frac{1}{\sqrt{y}}$

And there we have it! The inverse quartic equation $y=x^{-4}$ is tautochronous such that the time taken to empty the tank is independent of the 'depth' of the water column.

Because the $x$-axis is asymptotic to the inverse quartic curve, we should also ensure that the tank holds a finite volume of water of water for a given height of discharge. But it's an easy exercise to check that the volume is indeed finite.

Hope you enjoyed this. See ya soon.

Until then, Yours Aye

Me